You-Youスクールあすみが丘

昨日までは100ます計算を3ヶ月ほど取り組んできた成果についてお伝えしましたが、今日は課題についてです。

100ます計算を取り組みはじめて、どの生徒も点数が上がって、タイムも短くなってきたのですが、その成長が緩やかな生徒がいます。

すでに計算が大嫌いになっている生徒です。

自宅で練習してくることがほとんどないので、あまり成果が上がってきません。

「家でも練習してくると、タイムも良くなるよ」などと、毎回促していますが、なかなかやってくることができません。

こうした生徒にどのように働きかけるといいのか、どうしたら前向きに取り組めるようになるのかというのが現在の課題です。

100ます計算については、また報告したいと思います。

100ます計算を3ヶ月やってみて、生徒たちの様々な様子に出会っています。

まず、計算自体が速く正確になってきました。

これが100ます計算に取り組む目的でしたので、3ヶ月前より生徒の計算力が向上してきてとても嬉しいです。

また点数が上がったり、タイムが短くなったりした時には、生徒自身も自分の成長を実感しやすいようです。

子どもたちは3秒は早くなっただけでも、とても喜んでいます。

努力をするとわりと簡単に成果が現れるので、努力と成果を結びつけやすくなっています。これが小学生には合っているように思います。

授業だけでなく、自宅でも練習すると成果が出るというのがわかってきたようで、自宅でも練習してくる生徒が増えています。

他にも良い成果が見られます。

100ます計算は授業の初めに取り組んでいますが、最初に100ますをやることで、その後の授業を集中して臨む生徒が増えてきました。

100ます計算は以前もやっていたことがあったので、授業にも良い影響があることは分かっていましたが、改めて実感しています。

きっと、授業の最初に頭をフル回転させるので、頭がいい状態のまま、その後の授業も過ごせるようです。

まるで車のエンジンのようです。

以前、小学生4年生〜6年生の算数クラスで、100ます計算を再開したお話をしました。

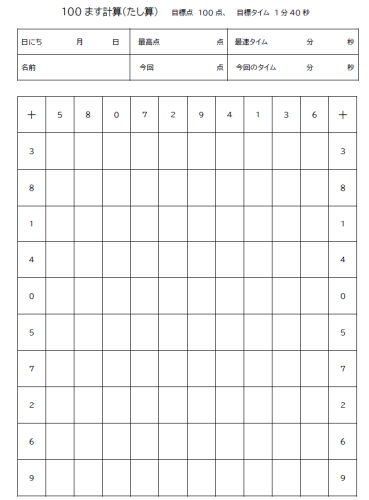
100ます計算は、名前の通り100ますの中に計算の答えを書いていく計算練習です。

1けたのたし算（例7+6）、20以内のひき算（例13-7）、かけ算（くく）、わり算がありますが、YouYouスクールあすみが丘では、全員がたし算からスタートしました。

そして、目標点と目標タイムを設定して、両方を同時にクリアしたら次のひき算に進みます。

目標点は100点（満点）、目標タイムは1分40秒にしています。

これは、1問を1秒で計算しなければならないスピードです。

100ます計算を再開して、もうすぐ3ヶ月ほど経ちますが、だんだんと練習の成果が現れてきました。

現在は数名の生徒が目標をクリアしてひき算に進み、もうすぐ目標をクリアできそうな生徒も増えてきています。

正に継続は力なりです。

明日は、100ます計算の良さについてお伝えしようと思います。

数とト・モ・ダ・チになる（３）の続きです。（１）（２）（３）を読んでいない方は、先にお読みください。

現在、100ます計算のたし算をやり始めて1か月ほど経ちました。残念ながら夏期講習中は時間が取れずできなかったのですが、早くも目標タイム、目標点をクリアした生徒が出始めています。目標タイムは1分40秒、目標点は100点です。

目標に達した生徒は、次のひき算に入りました。

まだ目標に届いていない生徒も、タイムが短くなってきました。タイムを1分以上短縮した生徒もいます。家庭学習でも取り組んでくる生徒は、目に見えて良くなっています。100ます計算は、練習した分だけ成果が上がるので、生徒が自分の練習の成果を認識しやすいのが特長です。そのため、はじめのうちは家庭学習で取り組まなかった生徒も、練習した分だけ結果が出ることを体験すると、家庭でも自ら取り組むようになってきます。

小学3年生以下の生徒は、50ます計算に取り組み始めました。

ます計算の成果については、またご紹介します。

数とト・モ・ダ・チになる（２）の続きです。（１）（２）を読んでいない方は、先にお読みください。

計算力がつき数と友だちになってくると、数の性質もだんだんと身についてきます。数の性質とは、その数が持っている特徴です。例えば36の場合、36がどんな数でわり切れるか（約数）、どんな数の積で表せるか（約数同士の積⇒1×36、2×18、3×12、4×9、6×6）、また２つ以上の数について同時に考える場合は、両方（すべて）の数に共通する性質は何か（偶数・奇数、公約数、最大公約数、公倍数、最小公倍数など）ということが、自然に見えてくるようになります。これが、数に対するセンスになります。

計算では、36×25 は 9×(4×25)＝9×100 = 900のように筆算をせず、暗算で瞬時に工夫して求められるようになります。分数を小数に直す（5/8＝0.625）、分数の約分する（36/54＝2/3）、異分母同士の分数を通分する（5/12と7/15の通分は25/60と28/60）など、こうした計算も素早く正確にできるようになります。

そして、小学生のうちに数と友だちになると、中学の数学もつまずくことはありません。

先ほど例に挙げた36×25 は6²×5²＝(6×5)²＝30²＝900のように累乗の計算に変形することもできます。また、X²－10X－56＝(X+4)(X-14)のように因数分解の数や文字の組み合わせを瞬時に見つけられたりするなど、数や式をスムーズに変形する能力や感覚が養われてきます。

こうした、数に対するセンスは、算数、数学を学んでいく上でとても大きな武器になります。

数と友だちになっていないと、このような式の変形にかなりの時間がかかり、学習進度が遅くなってしまいます。

小学低学年で習う計算の習熟度が、やがて中学の数学にも影響を及ぼしてくるので、できるだけ早く習熟度を高めていきたいと考えています。

数とト・モ・ダ・チになる（４）へ続く。